April 5th - No Class

No Class this weekend. Enjoy your time off.

---

You rock. That's why Blockbuster's offering you one month of Blockbuster Total Access, No Cost.

More on Euler Line

 

We stated in a previous class that the three centers of a triangle (circumcenter, centroid and orthocenter) falls on the same line (colinear) known as the Euler Line.

Let's now take a look at why this is true and what more we can learn about the Euler line.

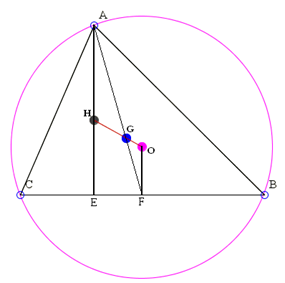In order to prove that these three centers (circumcenter O, centroid G, orthocenter) are colinear,  let's start by extending OG to meet the altitude AE at point H.
All we need to do is to prove that H is indeed the orthocenter.

Since  AE and OF are both perpendicular to BC, thus parallel to each other,  it goes that triangle AHG and GOF are similar.  It is well known that AG : GF = 2 : 1 because G is the centroid.  Thus we have
GH : GO =  AH : FO = 2 : 1

Let's connect C and H, and also draw the median CD going through G as below.

Since HG : GO = CG : GD = 2 : 1, we conclude that triangles CHG and GDO are similar, which implies that CH is parallel to OD. Thus CH is perpendicular to AB. This shows H is indeed the orthocenter.  We are done.

We further established that the distance between the centroid and orthocenter doubles that between the circumcenter and the centroid, with the centroid always lying between the other two centers.

March 29 - Homework

Homework for this week

Prove that the angular bisectors of the three angles of a triangle meets at one point, using Ceva's theorem.

Ceva's Theorem

 

Ceva's theorem states that for an arbitrary triangle ABC,  three lines drawn from each of the vertex of the triangle (AD, BE and CF ) meets at one point (the three lines are a.k.a. concurrent)   if and only if

Proof:   In order to relate these three ratios together,  we probably need to seek out (or create) some similar triangles.  Let's attempt this by drawing a parallel line through point A that is parallel to line BC.

Extend CF to cross this line at H,  extend BE to cross at G.

It is clear that triangles AGE and BCE are similar, so are AHF and BCF. Thus

Now we only need to figure out CD : DB.
Note that triangles AGK and BDK are similar, as are AHK and CDK.  Thus

Thus

Now this only proves that if AD, BE and CF are concurrent, the above equation holds.

We now go ahead to prove the 2nd half of Ceva's theorem, that if the above equation holds, then the three lines must be concurrent.  We use the approach of contradiction.  Assume that AD doesn't pass through the point of intersection K  between BE and CF,  as shown below.  Then we can always draw a line from A that passes through K and intersect line BC at point Q.

By the same logic as above, we can show that

Comparing this to the the known condition, we have

 
Add 1 to each side,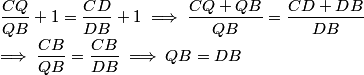

Thus Q and D must coincide, ie AD must pass through point K.  That proves the 2nd half of this theorem.

Centers of Triangles

 

There are a number of important centers for a triangle (any triangle).  These are:

The centroid - the point at which all three medians of a triangle meet.

The circumcenter: the point at which the perpedicular bisectors of the three sides meet.  This is the center of the "circumcircle",  the circle that passes through all three points of the triangle.

The incenter:  the point at which the three angular bisectors meet at one point,  which is the center of the "incircle", the circle that sits within the triangle, and tangent to all three sides of the triangle.

The orthocenter:  the point at which all three altitudes of the triangle meet.

These four centers (quartet) are the well known centers of a triangle, since the Greek times.  There is also an line known that connects three of these four centers, which includes the centroid, circumcenter and the orthocenter.  This line is known as the Euler Line.

March 29

We will move on to talk about other properties of the triangle. One of the more useful theorem concerns when three lines drawn from each of the vertex meet at one point.
This applies to the case of all kinds of centers for the triangle, the centroid, the incenter, the circumcenter, the orthocenter, so on and so forth.

Remember Damien demonstrated the proof of why the three medians of a traingle meet at one point, the centroid at the beginning of last class. We will study the commonality among all of these centers, and come up with a much easier way of proving that.
We'll attempt to prove the same for the other centers. And leave one for you to do as homework.

Law of Cosine

It's easy to see that ADBC is an isosceles trapezoid.  Apply Ptolemy's theorem

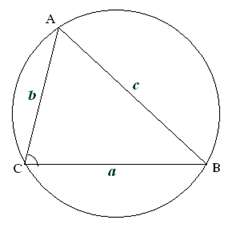For any triangle ABC as depicted, with length of a, b and c  for sides across ∠A, ∠B, and ∠C respectively,  the law of Cosine states that

 

There are multiple ways to prove this important theorem about triangles.

Here we will use the Ptolemy theorem we have studied to prove it.

Let's start by constructing a mirror ΔDBC of the original triangle ΔABC.

It's easy to see that ADBC is an isosceles trapezoid.  Apply Ptolemy's theorem to the cyclic quadrilateral ADBC, we have: