Proof of Ptolemy's Theorem

 

A recap of the proof of Ptolemy's theorem I did in class today. This is a well known proof.   Simple and constructive in nature.

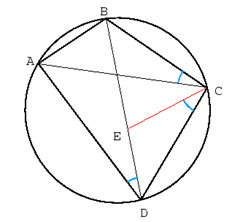
Given cyclic quadrilateral ABCD as shown. From point C, make line CE such that ∠ECD ≌ ∠BCA.

One can easily see that

ΔABC ∽ ΔDEC

which implies AB : DE = AC : DC ... (1)

Also because ΔCAD ∽ ΔCBE,
which implies BC : AC = BE : AD ... (2)

By (1) :   AB * DC = AC * DE

By (2) :  BC * AD = AC * BE     Adding these two equations gives

AB * DC + BC * AD = AC * DE + AC * BE = AC * (DE + BE) = AC * DB    Voila.