More on Euler Line

 

We stated in a previous class that the three centers of a triangle (circumcenter, centroid and orthocenter) falls on the same line (colinear) known as the Euler Line.

Let's now take a look at why this is true and what more we can learn about the Euler line.

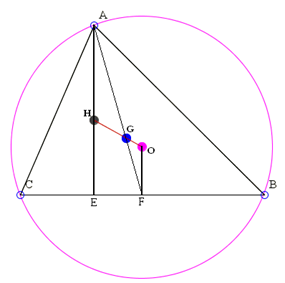In order to prove that these three centers (circumcenter O, centroid G, orthocenter) are colinear,  let's start by extending OG to meet the altitude AE at point H.
All we need to do is to prove that H is indeed the orthocenter.

Since  AE and OF are both perpendicular to BC, thus parallel to each other,  it goes that triangle AHG and GOF are similar.  It is well known that AG : GF = 2 : 1 because G is the centroid.  Thus we have
GH : GO =  AH : FO = 2 : 1

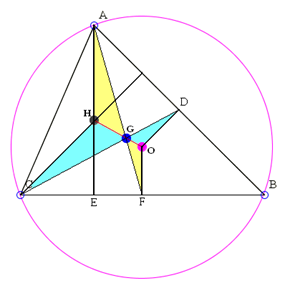
Let's connect C and H, and also draw the median CD going through G as below.

Since HG : GO = CG : GD = 2 : 1, we conclude that triangles CHG and GDO are similar, which implies that CH is parallel to OD. Thus CH is perpendicular to AB. This shows H is indeed the orthocenter.  We are done.

We further established that the distance between the centroid and orthocenter doubles that between the circumcenter and the centroid, with the centroid always lying between the other two centers.