Law of Cosine
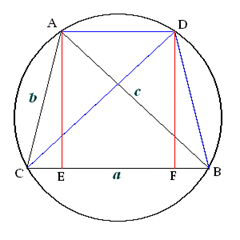
It's easy to see that ADBC is an isosceles trapezoid. Apply Ptolemy's theorem
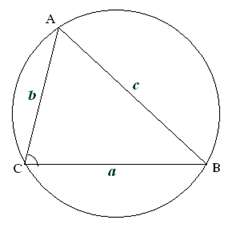 For any triangle ABC as depicted, with length of a, b and c for sides across ∠A, ∠B, and ∠C respectively, the law of Cosine states that
For any triangle ABC as depicted, with length of a, b and c for sides across ∠A, ∠B, and ∠C respectively, the law of Cosine states that
There are multiple ways to prove this important theorem about triangles.
Here we will use the Ptolemy theorem we have studied to prove it.
Let's start by constructing a mirror ΔDBC of the original triangle ΔABC.
It's easy to see that ADBC is an isosceles trapezoid. Apply Ptolemy's theorem to the cyclic quadrilateral ADBC, we have:
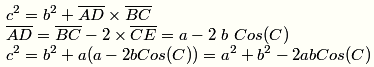

0 Comments:
Post a Comment
Subscribe to Post Comments [Atom]
<< Home