Centers of Triangles

 

There are a number of important centers for a triangle (any triangle).  These are:

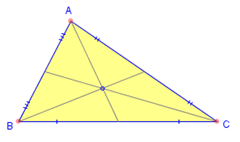
The centroid - the point at which all three medians of a triangle meet.

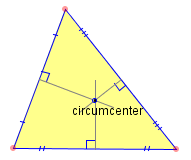
The circumcenter: the point at which the perpedicular bisectors of the three sides meet.  This is the center of the "circumcircle",  the circle that passes through all three points of the triangle.

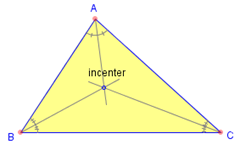
The incenter:  the point at which the three angular bisectors meet at one point,  which is the center of the "incircle", the circle that sits within the triangle, and tangent to all three sides of the triangle.

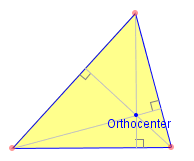
The orthocenter:  the point at which all three altitudes of the triangle meet.

These four centers (quartet) are the well known centers of a triangle, since the Greek times.  There is also an line known that connects three of these four centers, which includes the centroid, circumcenter and the orthocenter.  This line is known as the Euler Line.