Ceva's Theorem

 

Ceva's theorem states that for an arbitrary triangle ABC,  three lines drawn from each of the vertex of the triangle (AD, BE and CF ) meets at one point (the three lines are a.k.a. concurrent)   if and only if

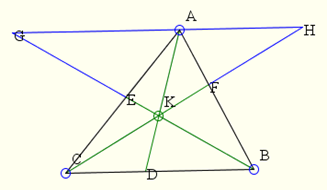
Proof:   In order to relate these three ratios together,  we probably need to seek out (or create) some similar triangles.  Let's attempt this by drawing a parallel line through point A that is parallel to line BC.

Extend CF to cross this line at H,  extend BE to cross at G.

It is clear that triangles AGE and BCE are similar, so are AHF and BCF. Thus

Now we only need to figure out CD : DB.
Note that triangles AGK and BDK are similar, as are AHK and CDK.  Thus

Thus

Now this only proves that if AD, BE and CF are concurrent, the above equation holds.

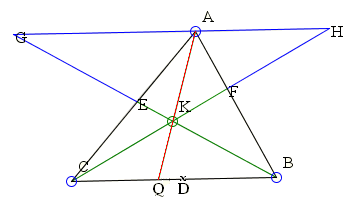
We now go ahead to prove the 2nd half of Ceva's theorem, that if the above equation holds, then the three lines must be concurrent.  We use the approach of contradiction.  Assume that AD doesn't pass through the point of intersection K  between BE and CF,  as shown below.  Then we can always draw a line from A that passes through K and intersect line BC at point Q.

By the same logic as above, we can show that

Comparing this to the the known condition, we have

 
Add 1 to each side,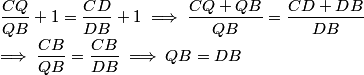

Thus Q and D must coincide, ie AD must pass through point K.  That proves the 2nd half of this theorem.